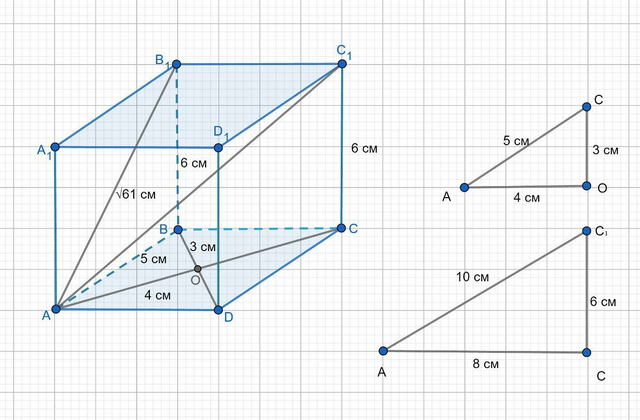
Диагонали ромба пресекаются под прямым углом и точкой пересечения делятся пополам. В основании параллелепипеда ромб, ΔAOB прямоугольный, катет AO = 8/2 = 4 см, катет BO = 6/2 = 3 см. Найдем сторону ромба AC по т. Пифагора из ΔAOB.
AB² = AO² + OC² = 4² + 3² = 16 + 9 = 25; AB = 5 см;
Из ΔABB₁ найдем высоту параллелепипеда по т.Пифагора.
B₁B² = AB₁² – AB² = 61-25 = 36; B₁B = 6 см;
Из ΔACC₁ найдем большую диагональ параллелепипеда AC₁² = AC² + CC₁² = 8² + 6² = 64 + 36 = 100;
Большая диагональ параллелепипеда AC₁= 10 см;
Боковая поверхность параллелепипеда произведению периметра основания на высоту параллелепипеда:
S = P*H = 4*5 см * 6 см = 120 см².