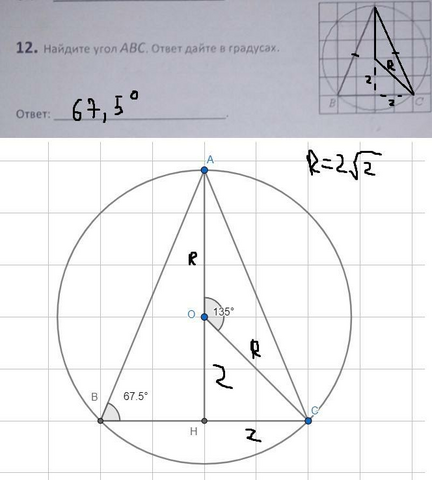
На самом деле очень сложное задание, я бы будучи в 9 классе на огэ не решил бы такое скорее всего:
------------
По т. пифагора найдем радиус:

----------------
Найдем высоту:

----------------
Теперь по т. Пифагора найдем AC:

Пока оставим так...
---------------
теперь запишем теорему косинусов для треугольника AOC:

Это табличное значение косинуса:
α=135°
---------------
угол ABC=α/2=67,5° (так-как это вписанный угол который опирается на дугу AC)
Ответ 67,5°
---------------
Если что-то непонятно, задай вопрос.