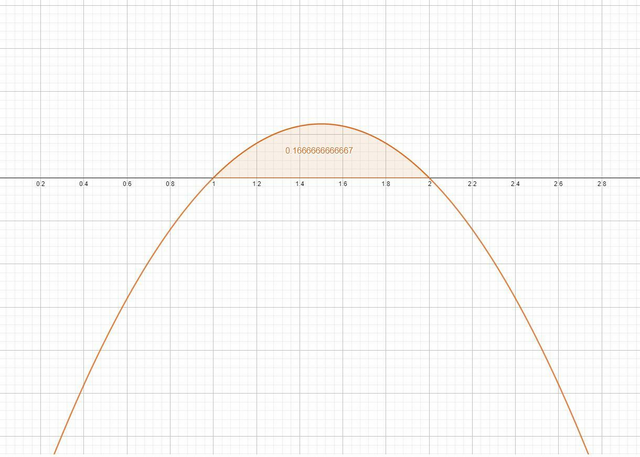
площадь под графиком функции, есть определенный интеграл:
-x^2+3x-2 -это парабола с ветвями вниз и корнями, которая пересекает ось абсцисс в точках 2 и 1 (по теореме виета) см. рисунок.
![\int\limits^2_1 {-x^2+3x-2} \, (dx) =-\frac{x^3}{3}+\frac{3x^2}{2}-2x |[1;2]=\\=(-\frac{8}{3}+6-4 )-(-\frac{1}{3}+\frac{3}{2}-2)=\\=(-\frac{2}{3} )-(-\frac{5}{6} )=\frac{5-4}{6}=\frac{1}{6} \int\limits^2_1 {-x^2+3x-2} \, (dx) =-\frac{x^3}{3}+\frac{3x^2}{2}-2x |[1;2]=\\=(-\frac{8}{3}+6-4 )-(-\frac{1}{3}+\frac{3}{2}-2)=\\=(-\frac{2}{3} )-(-\frac{5}{6} )=\frac{5-4}{6}=\frac{1}{6}](https://tex.z-dn.net/?f=%5Cint%5Climits%5E2_1%20%7B-x%5E2%2B3x-2%7D%20%5C%2C%20%28dx%29%20%3D-%5Cfrac%7Bx%5E3%7D%7B3%7D%2B%5Cfrac%7B3x%5E2%7D%7B2%7D-2x%20%20%7C%5B1%3B2%5D%3D%5C%5C%3D%28-%5Cfrac%7B8%7D%7B3%7D%2B6-4%20%29-%28-%5Cfrac%7B1%7D%7B3%7D%2B%5Cfrac%7B3%7D%7B2%7D-2%29%3D%5C%5C%3D%28-%5Cfrac%7B2%7D%7B3%7D%20%29-%28-%5Cfrac%7B5%7D%7B6%7D%20%29%3D%5Cfrac%7B5-4%7D%7B6%7D%3D%5Cfrac%7B1%7D%7B6%7D)
Ответ (1/6)
-------------------------
Ты в 10 классе интегралы решаешь или тебя заставили под конец 11?