Дана трапеция ABCD с основаниями AD и BC. Точки M и N лежат ** сторонах AB и CD...

Question

Дана трапеция ABCD с основаниями AD и BC. Точки M и N лежат на сторонах AB и CD соответственно, причём отрезок MN параллелен основаниям трапеции. Диагональ AC пересекает этот отрезок в точке O. Известно, что площади треугольников AMO и CNO равны. а) Доказать, что CM║AN. б) Найдите MN, если AD = a и BC = b.

Answer 1

Вариант решения:

а) S amo = S cno - по условию

S amo = (1/2)•MO•AO•sin∠AOM

S cno = (1/2)•NO•CO•sin∠CON

∠AOM = ∠CON - как вертикальные ⇒ MO•AO = NO•CO ⇒

MO/NO = CO/AO = k

∠MOC = ∠AON - как вертикальные ⇒ ΔМОС подобен ΔAON по двум пропорциональным сторонам и углу между ними ⇒ ∠ОМС = ∠ОNA - накрест лежащие углы ⇒ СМ || AN, ч.т.д.

б) Пусть NO = x, AO = y. Тогда МО = kx, CO = ky

ΔAMO подобен ΔАВС:   MO/BC = AO/AC

kx/a = y/(y+ky) = y/y(1+k) = 1/(k+1) ⇒ x/a = 1/k(k+1)

ΔOCN подобен ΔACD:  NO/AD = CO/AC

x/b = ky/(y+ky) = k/(k+1)

Заметим, b/a = (x/a)•(b/x) = ( 1/k(k+1) ) • (k+1)/k = 1/k²

⇒ k = √(a/b)

MN = kx + x = x(k+1)  ;  x = a/k(k+1)

MN = a•(k+1) / k(k+1) = a/k = a • √(a/b) = √(ab)

ОТВЕТ: б) √(аb)

---

Answer 2

Ответ: MN=√ab

Объяснение:

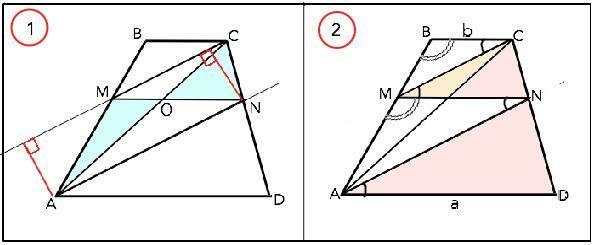
Рассмотрим рисунки приложения.

а) Примем площади равновеликих ( по условию) треугольников АМО и NСO равными m, а площадь ∆ МОС=k.  Тогда S(АМС)=m+ k, S(NMC)=m+k, ⇒ S(АМС)=S(NMC). Оба эти треугольника имеют общее основание МС, следовательно, их высоты (на рисунке они выделены красным цветом) равны.  ⇒ расстояние между точками А  и N и прямой МС равны ⇒ МС||АN. Доказано.

б) На основании параллельности ВС║MN║AD и MC║AN с общими секущими ∆ МВС~ ∆ АMN. Из подобия следует отношение а:MN=МС:АС. Аналогично ∆ МСN~∆AND ⇒ MN:b=MC:AC, из чего следует  а:MN=MN:b и MN²=ab, ⇒ MN=√ab

---