В равнобедренном треугольнике АВС внешний угол при вершине А равен 50°. Луч АА1 –...

Question

В равнобедренном треугольнике АВС внешний угол при вершине А равен 50°. Луч АА1 – биссектриса этого угла. Биссектриса угла АВС, пересекает прямую АА1, в точке М. Найдите длину отрезка АМ, если сторона АС=15 см.Сделайте рисунок пожалуйста и ответьте на вопром​

Answer 1

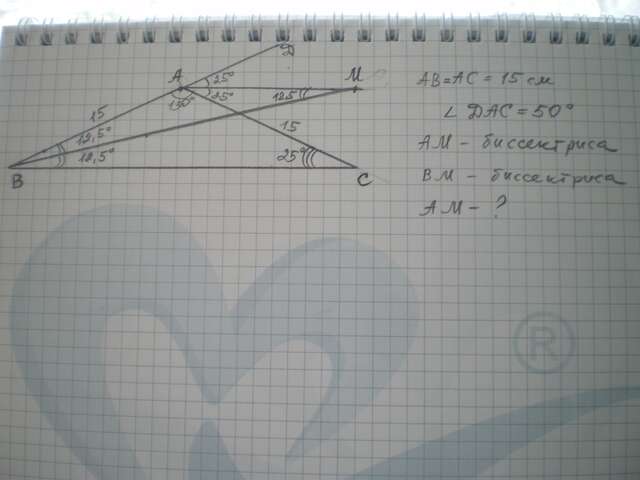
Ответ:

15 см.

Объяснение:

∠ВАС=180-∠ДАС=180-50=130° (по свойству смежных углов)

∠С=∠АВС=(180-130):2=25°

∠АВМ=∠СВМ=25:2=12,5°

∠ДАМ=∠МАС=50:2=25°

Рассмотрим ΔАВМ.   ∠ВАМ=∠ВАС+∠МАС=130+25=155°;

∠АМВ=180-∠ВАМ-∠АВМ=180-155-12,5=12,5°

значит, ΔАМВ - равнобедренный и АМ=АС=15 см.

---