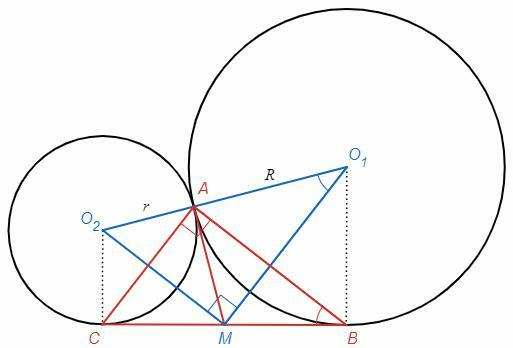
AM - общая касательная
MA=MB=MC (отрезки касательных из одной точки)
△ABC - прямоугольный (медиана равна половине стороны)
∠ABC=∪AB/2=∠MO1O2 (O1M - биссектриса ∠AO1B)
Аналогично ∠ACB =∠MO2O1
△ABC~△MO1O2 (по двум углам)
O1A=R =8, O2A=r =2
MA=√(Rr) (высота из прямого угла)
S△MO1O2 =(R+r)√(Rr)/2
S△ABC/S△MO1O2 =( 2√(Rr)/(R+r) )^2
S△ABC =(R+r)√(Rr)/2 *4Rr/(R+r)^2 =2Rr√(Rr)/(R+r) =2*16*4/10 =12,8