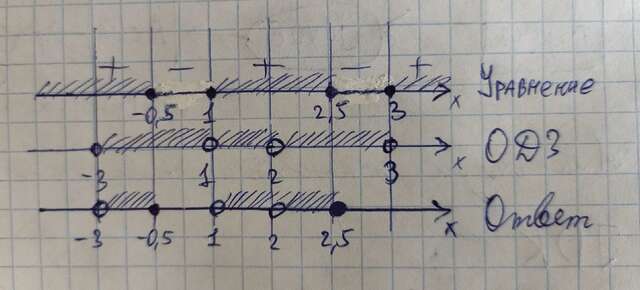
Ответ:
![x \in (-3;-0.5]\cup (1;2)\cup (2;2.5] x \in (-3;-0.5]\cup (1;2)\cup (2;2.5]](https://tex.z-dn.net/?f=x%20%5Cin%20%28-3%3B-0.5%5D%5Ccup%20%281%3B2%29%5Ccup%20%282%3B2.5%5D)
Пошаговое объяснение:

и используя метод интервалов + ОДЗ получим ответ.
Пояснения:
1)  : график "корыто", ветви вниз, тангенс наклона по модулю равен 2, основание
: график "корыто", ветви вниз, тангенс наклона по модулю равен 2, основание  , абсциссы точек углов
, абсциссы точек углов  , поэтому пересечения Ox при
, поэтому пересечения Ox при  , поэтому:
, поэтому:
2) ОДЗ:
 0\\ |x-2|\neq 1\\ 3-|x|>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}x > -3\\ x \neq 1\\ x \neq 2\\ x < 3\end{matrix}\right. \Leftrightarrow x\in (-3;1)\cup (1;2)\cup (2;3)" alt="\left\{\begin{matrix}|x-2|>0\\ |x-2|\neq 1\\ 3-|x|>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}x > -3\\ x \neq 1\\ x \neq 2\\ x < 3\end{matrix}\right. \Leftrightarrow x\in (-3;1)\cup (1;2)\cup (2;3)" align="absmiddle" class="latex-formula">
0\\ |x-2|\neq 1\\ 3-|x|>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}x > -3\\ x \neq 1\\ x \neq 2\\ x < 3\end{matrix}\right. \Leftrightarrow x\in (-3;1)\cup (1;2)\cup (2;3)" alt="\left\{\begin{matrix}|x-2|>0\\ |x-2|\neq 1\\ 3-|x|>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}x > -3\\ x \neq 1\\ x \neq 2\\ x < 3\end{matrix}\right. \Leftrightarrow x\in (-3;1)\cup (1;2)\cup (2;3)" align="absmiddle" class="latex-formula">
3) Метод интервалов: см. прикрепленный файл