x\;\bigg|-x \quad }} \right. \\\\\left \{ {{x(x-3)+2(x-3)\geq 0} \atop {5-3x-3-x>0\qquad }} \right. \\\\\left \{ {{(x-3)(x+2)\geq 0} \atop {2>4x\qquad \qquad \quad }} \right. \\\\\left \{ {{(x+2)(x-3)\geq 0} \atop {x<0,\! 5\qquad \qquad \quad}} \right." alt="\displaystyle \left \{ {{-x^2+x+6\leq 0\;\bigg|\cdot (-1)} \atop {5-3(x+1)>x\;\bigg|-x \quad }} \right. \\\\\left \{ {{x(x-3)+2(x-3)\geq 0} \atop {5-3x-3-x>0\qquad }} \right. \\\\\left \{ {{(x-3)(x+2)\geq 0} \atop {2>4x\qquad \qquad \quad }} \right. \\\\\left \{ {{(x+2)(x-3)\geq 0} \atop {x<0,\! 5\qquad \qquad \quad}} \right." align="absmiddle" class="latex-formula">
x\;\bigg|-x \quad }} \right. \\\\\left \{ {{x(x-3)+2(x-3)\geq 0} \atop {5-3x-3-x>0\qquad }} \right. \\\\\left \{ {{(x-3)(x+2)\geq 0} \atop {2>4x\qquad \qquad \quad }} \right. \\\\\left \{ {{(x+2)(x-3)\geq 0} \atop {x<0,\! 5\qquad \qquad \quad}} \right." alt="\displaystyle \left \{ {{-x^2+x+6\leq 0\;\bigg|\cdot (-1)} \atop {5-3(x+1)>x\;\bigg|-x \quad }} \right. \\\\\left \{ {{x(x-3)+2(x-3)\geq 0} \atop {5-3x-3-x>0\qquad }} \right. \\\\\left \{ {{(x-3)(x+2)\geq 0} \atop {2>4x\qquad \qquad \quad }} \right. \\\\\left \{ {{(x+2)(x-3)\geq 0} \atop {x<0,\! 5\qquad \qquad \quad}} \right." align="absmiddle" class="latex-formula">
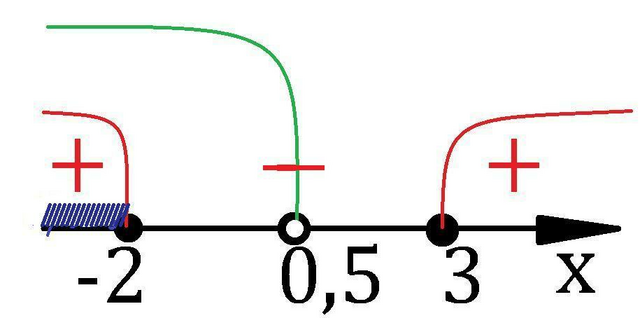
Решим методом интервалов верхнее неравенство системы и сразу же наложим условие нижнего нер-ва.
См. внизу.
Ответ: x∈(-∞;-2].