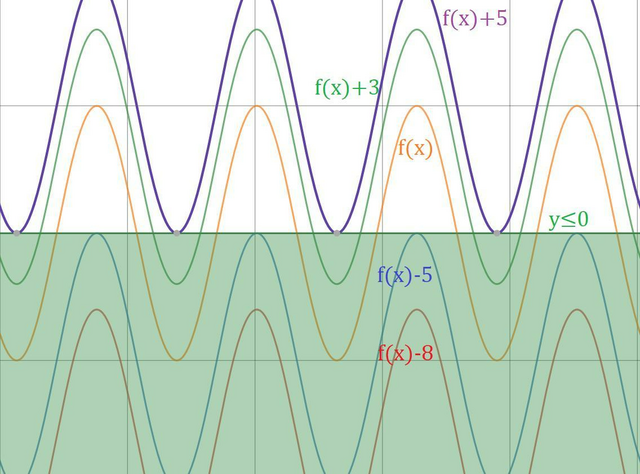
Графиком этой функции является cosx, который растянут в 5 раз по ординате, смещён влево на arccos 0.8 и перевёрнут. Главное, что максимальное и минимальное ЗНАЧЕНИЕ это 5 и -5 т.к. |cosx|≤1.
Так вот если рассматривать функцию y=f(x)+p, то когда |p|=5 график Y будет касаться оси Ох своими экстремумами, соответственное когда p<-5, то график будет полностью ниже Ох, то есть <0, а когда p>5 --> y>0. Нам необходимо, чтобы касаний было хотя бы одно (от 1 до бесконечности), а учитывая, что знак ≤, то имеем:
f(x)+p≤0, при p≤5, а значит если f(x)≤a, то a≤-5.
Для ясности картины смотри вниз.
Ответ: a∈(-∞;-5]