Ответ:
54 см²
Объяснение:
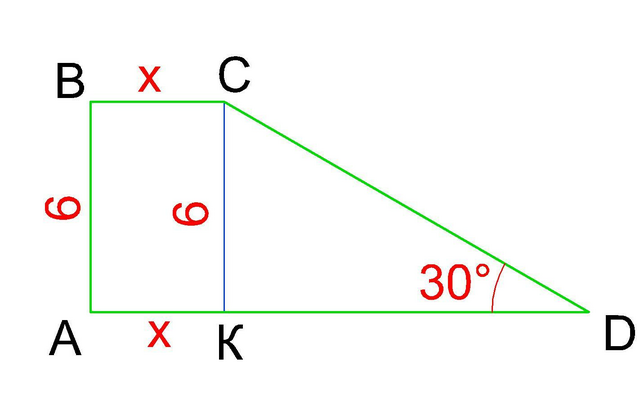
Позначимо трапецію як АВСД, та висоту із вершини С на основу АД як СК.
Площа прямокутної трапеції складається із площини прямокутника АВСК та площини прямокутного ΔСДК.
Позначимо верхню основу за х, тоді ВС=АК=х і площа АВСК дорівнює СК*ВС=6х; нижня основа трапеції АД=АК+КД=х+КД
В прямокутному ΔСДК відомий катет СК=6 - протилежний куту Д=30°, тому катет КД=СК·ctg∠D=6√3,
в свою чергу гіпотенуза СД=СК÷sin∠D=6·2=12.
Відомо, що, якщо в трапецію можна вписати коло, то сума довжин її осно дорівнює сумі довжин її бічних сторін.
Тоді отримуемо рівняння: ВС+АД=АВ+СД ⇒
х+х+6√3=6+12
х=3·(3-√3)
Тоді площа трапеції: