Дано: F(x) = cos(6x) + sin(6x) Xo = π/8 = 22.5°
Найти: Уравнение касательной.
Пошаговое объяснение:
Y = k*x+ b = F'(Xo)*(x - Xo) + F(Xo) - уравнение касательной.
Находим первую производную функции.
F'(x) = - 6*sin6*x + 6*cos6*x.
Вычисляем в точке Хо = π/8, 6*Xo = 3/4*π
F'(x) = k = - 3√2 - 3√2 = - 6√2 - наклон прямой.
Вычисляем значение функции в точке Хо.
F(Xo) = cos(3/4*π) + sin(3/4*π) = -√2/2 + √2/2 = 0
b = -k*(Xo) = 6√2*π/8 = 3/4*√2*π
Ответ: Y = -6√2*x + 3/4*√2*π - уравнение касательной.
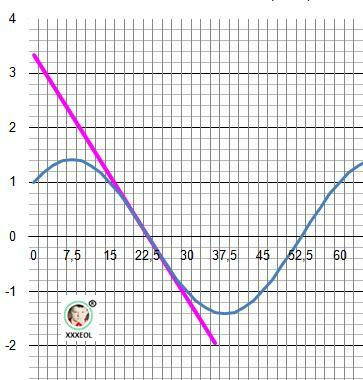
Дополнительно: рисунок с графиками в приложении.