Ответ:
45°
Объяснение:
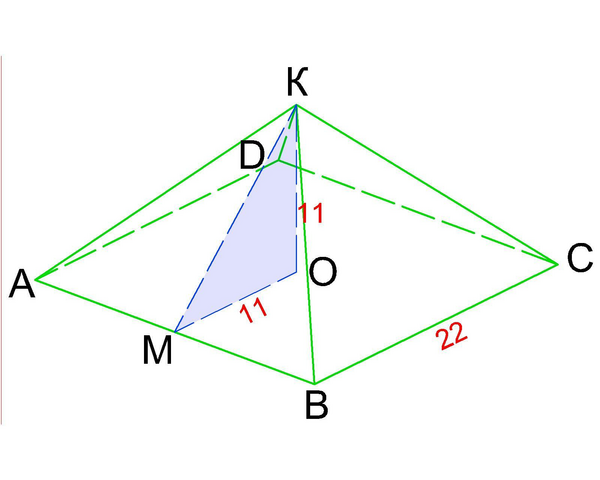
Обозначим основание пирамиды как квадрат АВСД, центр пересечения диагоналей квадрата - т.О, вершина пирамиды - т.К, высота пирамиды - отрезок КО, высота из т.О на сторону АВ основания - отрезок ОМ.
Тогда угол, который образует боковая грань с плоскостью основания будет равен ∠КМО в прямоугольном ΔКМО с катетами ОМ и КО.
Катет КО = 11 см по условию задачи,
катет ОМ равен радиусу вписанной в квадрат основания окружности, поэтому равен половине стороны основания, т.е.
ОМ=22/2=11 см.
Т.к. оба катета равны, то получаем прямоугольный равнобедренный треугольник, с углами при гипотенузе ∠КМО=∠МКО=45°