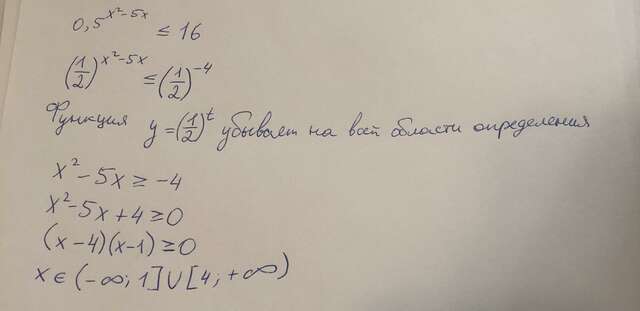Поясню моменты, которые могли оказаться непонятными:
1) я быстро раскладываю квадратный трёхчлен на множители, там теорема Виета в помощь (сумма корней равна пяти, произведение четырём) или дискриминант в крайнем случае
2) так же быстро решаю неравенство в последней строчке. Всё дело в том, что график функции y=x^2-5x+4 - парабола ветвями вверх, у функции два нуля, значит, она имеет знак + слева от меньшего её нуля и справа от большего. Можно также аккуратно подставлять и считать знаки на промежутках.
3) Ну и знак неравенства после соответствующего пояснения меняется в связи с тем, что основание степени (1/2) меньше одного, а значит большее значение аргумента соответствует меньшему значению функции.