Дана прямая треугольная призма ABCA1B1C1. AC=3, AB=5, угол CAB=120 градусов Scc1b1b=35...

Question

Дана прямая треугольная призма ABCA1B1C1. AC=3, AB=5, угол CAB=120 градусов Scc1b1b=35 Найти площадь боковой поверхностиЕсли можно, то еще и рисунок

Answer 1

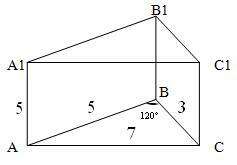
AB=5 см, BC=3 см, ∠ABC=120°, S(AA1C1C)=35 см²

По т. косинусов AC² = AB² + BC² - 2*AB*BC*cos 120°

AC²=25+9-2*5*3*(-1/2)=34+15=49 => AC=7 см (бОльшая сторона треугольника)

S(AA1C1C)=AA1*AC=AA1*7=35 => AA1=5 см (высота призмы)

Sбок. =S(AA1B1B)+S(BB1C1C)+S(AA1C1C)=5*5+3*5+7*5=25+15+35=75 см²

Ответ: 75 см².

Вроде так

---

Comments

а почему BC стала равняться 3?