30 баллов. В прямоугольном треугольнике (∠A = 90°) величина угла B составляет 30°. Из...

Question

30 баллов. В прямоугольном треугольнике (∠A = 90°) величина угла B составляет 30°. Из вершины угла C проведена биссектриса CD, которая разбивает противоположный катет на отрезки AD и BD. докажите, что ∆ABC ~ ∆ACD; найдите отношение AD : BD.

Answer 1

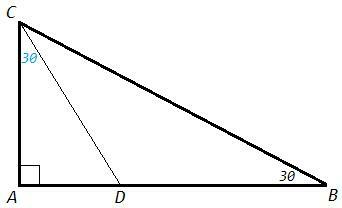
Сумма острых углов прямоугольного треугольника 90.

С=90-B=90-30=60

Биссектриса делит угол пополам.

ACD=C/2=60/2=30

Треугольники ABC и ACD подобны по двум углам.

Катет против угла 30 равен половине гипотенузы.

AC=BC/2

Биссектриса делит сторону в отношении прилежащих сторон (теорема о биссектрисе).

AD/BD = AC/BC =1/2

---