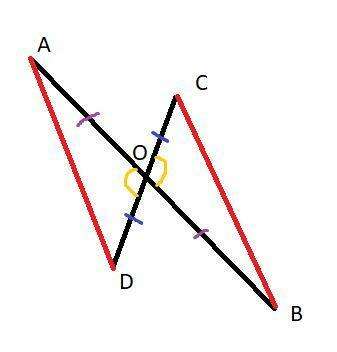
Смотри приложение
Пусть AB пересекает CD в точке О, так что AO=OB и CO=OD
Тогда ∠AOD=∠COB как вертикальные
Следовательно, ΔAOD=ΔCOB по двум равным сторонам и углу между ними.
Теперь можно утверждать, что ∠ODA=∠OCB как соответственные части равных треугольников
А эти углы накрест лежащие при отрезках AD и CB и секущей CD
Следовательно, прямые параллельны, так как накрест лежащие углы равны