Дано:
 км
км
 км
км
 t_{2}-t_{1}=2" alt="t_{1}=t_{2} -2 => t_{2}-t_{1}=2" align="absmiddle" class="latex-formula">
t_{2}-t_{1}=2" alt="t_{1}=t_{2} -2 => t_{2}-t_{1}=2" align="absmiddle" class="latex-formula">
\
Найти:

Решение:
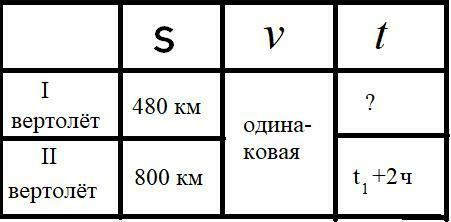
Условие задачи можно также представить в виде таблицы (см. рисунок), по которой можно понять, что решить задачу нужно с помощью уравнения.
Формулы, используемые в задаче: 
1) Чтобы составить уравнение, нам нужно найти какую-то величину, которая и у I вертолета, и у II вертолёта равна, и это скорость.
Выводим формулы скорости у каждого вертолёта: у первого получится  , у второго -
, у второго -  (за единицу t мы взяли
(за единицу t мы взяли  , а
, а  представили как t+2.
представили как t+2.
Получаем уравнение:

Решаем его методом пропорций:

Раскрываем скобки во второй части уравнения:

Перемещаем 480t в первую часть уравнения из второй, меняя при этом знак на противоположный (то есть на минус)

Дальше решаем как стандартное уравнение:

Ура, мы нашли  ч. Осталось найти
ч. Осталось найти 
2) Из пункта Дано знаем, что  , следовательно:
, следовательно:
 ч
ч
Ответ:  ч;
ч;  ч
ч