Ответ:
Расстояния до сторон треугольника 13 см.
Пошаговое объяснение:
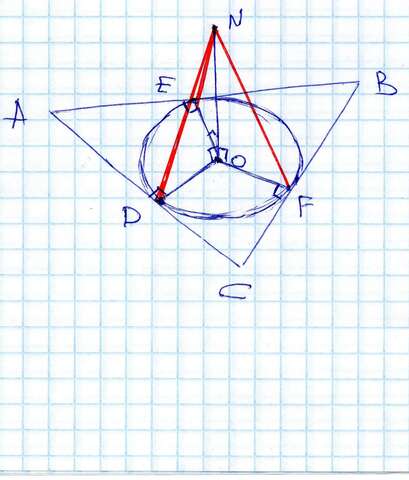
Расстоянием от точки N сторон треугольника будут перпендикуляры ND, NF и NE опущенные на эти стороны из точки N.
ND, NF и NE будут перпендикулярны ON, так как лежат в плоскости треугольника, а он перпендикулярен высоте ON
ND, NF и NE будут перпендикулярны соответствующим сторонам AD, CB и AB, кроме того ND = NF = NE = r (радиусу вписанной окружности)
Полученные треугольники NOD, NOF и NOE ,будут прямоугольными и равными (по двум катетам) следовательно чтобы найти расстояние от точки N до всех сторон, достаточно найди любую гипотенузу, наример NF.
По теореме Пифагора
NF²=OD²+ON² ,
OD = 5 см есть радиус вписанной окружности, ON = 12 см
NF=√169=13 см.
ND = NF = NE =13 см.