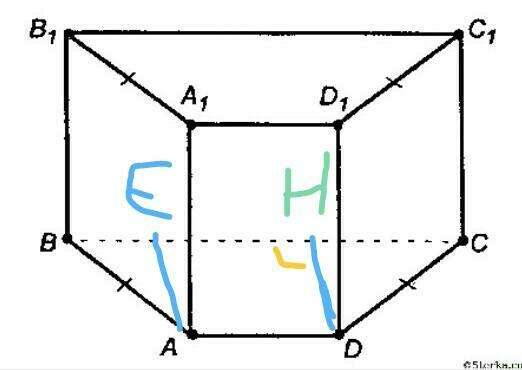
Дано: АВСДА1В1С1Д1- прямая призма, АВСД - трапеция, АД=ДС, ВС=4 см, АД=3 см, АА1=38 см, ДН=2 см.
Найти: Sполн.
Решение:
Sполн=Sбок+2Sосн.
Sбок=h×Росн
Рассм. трапецию АВСД:
Проведем высоты АЕ и НД, тогда АЕНД - прямоугольник и АД=ЕН. Т.к. трапеция равнобокая, то ВЕ+НС=4-ЕН=4-3=1 см. ВЕ=НС=0,5 см.
Рассм. треуг. НДС:
угол Н=90 градусов, НД=2см, НС=0,5 см. По т. Пифагора найдем СД:

Sосн=h×(ВС+АД)/2 = 2× (3+4)/2 = 2×3,5=7 (см^2).
Sбок=

S полн=

Ответ: