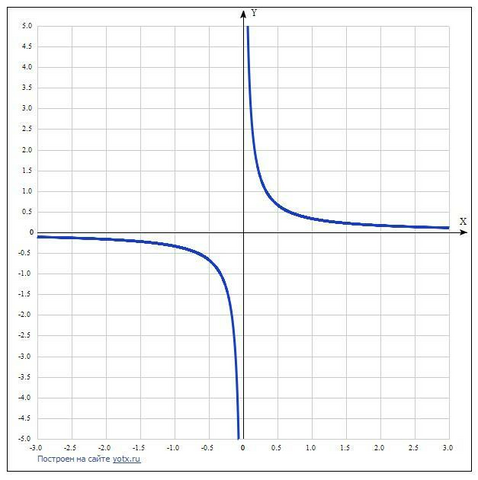
Решение:
1) Функция определена повсюду кроме точки, в которой знаменатель превращается в ноль, x = 0.
Область определения состоит из двух интервалов D(y):(-∞;0) U (0; +∞).
2) Так как функция не имеет значения при х = 0, то график функции не пересекает ось Оу.
Приравняем функцию к нулю:
1/3x=0.
Так как эта функция не может быть равна 0, то график функции не пересекает ось Ох:
3) Проверяем функцию на четность.
Проверим функцию - четна или нечетна с помощью соотношений f(x)=f(-x) и f(x)=-f(x). Итак, проверяем:
f(-x)=1/(3*(-x))=-1/3x≠f(x)=-f(x).
Итак, функция нечетная, непериодическая.
4) В данном случае имеем одну точку разрыва x=0.
Вычислим границы слева и справа от этой точки
lim┬(x→-0)〖 1/3x=-∞.〗
lim┬(x→+0)〖 1/3x=+∞.〗
Итак, x=0 – точка разрыва второго рода.
5) Для отыскания интервалов монотонности вычисляем первую производную функции
〖y^'=〗〖1/3* -1/x^2 =-1/〖3x〗^2 =0.〗
Решаем это уравнение и его корни будут экстремумами, но так как переменная только в знаменателе, то производная не может быть равна нулю.
Поэтому функция не имеет экстремумов.
Поскольку при любых значениях аргумента производная отрицательна, то функция на всей области убывающая.
6. Точки перегибов графика функции:
Найдем точки перегибов для функции, для этого надо решить уравнение y''=0 - вторая производная равняется нулю, корни полученного уравнения будут точками перегибов указанного графика функции, + нужно подсчитать пределы y'' при аргументе, стремящемся к точкам неопределенности функции:
y''((1/(3x)) = 2/(3x³) = 0
Данная функция не может быть равна нулю, поэтому перегибов у функции нет.
7) Интервалы выпуклости и вогнутости.
Интервалы, где функция выпуклая или вогнутая, находим по знаку второй производной : где вторая производная меньше нуля, там график функции выпуклый, а где больше - вогнутый.
x = -1 0 1
y'' = -2/3 -2/3.
Вогнутая на промежутках: (0; ∞)
Выпуклая на промежутках: (-∞;0)
8) Асимптоты.
Вертикальной асимптотой является ось Оу, определённая в пункте 4.
Горизонтальные асимптоты графика функции:
Горизонтальную асимптоту найдем с помощью предела данной функции при x->+∞ и x->-∞. Соотвествующие пределы находим:
lim┬(x→∞)〖 1/3x=∞〗, значит, горизонтальной асимптоты справа не существует.
Аналогично, при x->-∞ f(x) = -∞, значит, горизонтальной асимптоты слева не существует
Наклонные асимптоты графика функции.
Уравнение наклонной асимптоты имеет вид y=kx+b. Наклонную асимптоту можно найти, подсчитав предел данной функции, деленной на x при lim┬( x→±∞)〖(kx+b-f(x)).〗
Находим коэффициент k: k=lim┬(x→±∞)〖(f(x))/x.〗
k=lim┬( x→±∞)〖 1/(3x*x)=1/〖3x〗^2 =0.〗
Коэффициент b: b=〖lim┬(x→±∞) (〗〖f(x)-kx).〗
Для данной функции первый из этих пределов равен нулю, поэтому наклонная линия не определяется (она совпадает с горизонтальной асимптотой).
8) На основе проведенного анализа выполняем построение графика функции. Для этого сначала строим вертикальные и наклонные асимптоты, затем находим значение функции в нескольких точках и по них проводим построение.
Таблица точек
xy
-3.0-0.11
-2.5-0.13
-2.0-0.17
-1.5-0.22
-1.0-0.33
-0.5-0.67
0-
0.50.67
1.00.33
1.50.22
2.00.17
2.50.13
3.00.11.