Ответ: 8 дм и 6 дм
Объяснение: Основание правильной шестиугольной призмы - правильный шестиугольник. Её боковая поверхность состоит из 6-ти равных прямоугольников. Площадь каждого 288:6=48 дм²
Решение:
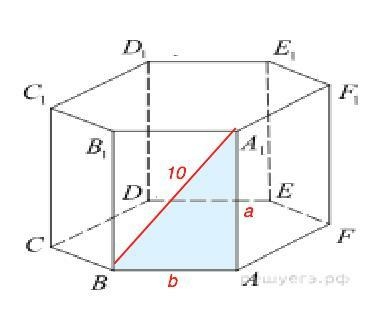
Способ 1). Площадь каждой грани равна произведению сторон прямоугольника. Рассмотрим грань АВВ1А1. Диагональ ВА1=10, она делит грань на два равных прямоугольных треугольника, в которых является гипотенузой. Следовательно, каждая из сторон грани не может быть больше или равна 10. Примем стороны грани равными а и b. Тогда при а<10>b имеем а•b=48=6•8. С диагональю грани эти числа составляют египетский треугольник, что соответствует условию. При этом как сторона может быть 6 дм, а высота 8 дм, так и наоборот: сторона 8 дм, высота 6 дм.
Способ 2). –––––––––––––––––––––––––––––––––––––––––––
По т.Пифагора с²=а²+b², откуда b=√(c²-a²). По условию с=10
S=a•b =48
a•√(10²-a²)=48² Возведем обе стороны уравнения в квадрат.
a²•(100-a²)=2403 ⇒ 100а²-а⁴=2403 ⇒ а⁴-100а²+2403
Примем а²= х. Тогда уравнение примет вид х²-100х+2403. Решив квадратное уравнение, получим х₁=64, х₂=36 ⇒ а₁=√64=8 (дм); a₂=√36=6 (дм)
Стороны грани равны 8 дм и 6 дм. Каждое из этих значений может быть как стороной, так и высотой данной призмы.