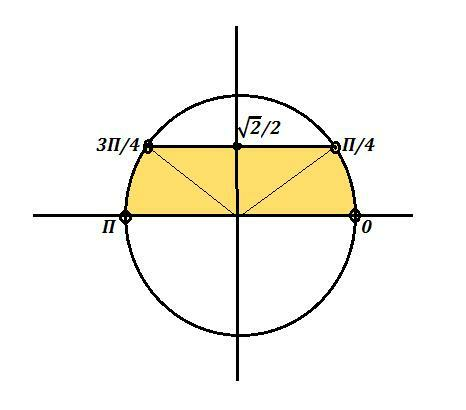
2\\\\2(1-sin^2x)+\sqrt2\, sinx-2>0\\\\2-2\, sin^2x+\sqrt2\, sinx-2>0\\\\2sin^2x-\sqrt2\, sinx<0\\\\\sqrt2\, sinx\cdot (\sqrt2\, sinx-1)<0\\\\t=sinx\; ,\; |t|\leq 1\; \; ,\; \; \sqrt2\, t\cdot (\sqrt2\, t-1)<0\; \; ,\; \; +++(0)---(\frac{1}{\sqrt2} )+++\\\\0<t<\frac{1}{\sqrt2} \; \; \; \Rightarrow \; \; 0<sinx<\frac{\sqrt2}{2}\; \; \Rightarrow \; \; \left \{ {{sinx>0} \atop {sinx<\frac{\sqrt2}{2}}} \right." alt="2\, cos^2x+\sqrt2\, sinx>2\\\\2(1-sin^2x)+\sqrt2\, sinx-2>0\\\\2-2\, sin^2x+\sqrt2\, sinx-2>0\\\\2sin^2x-\sqrt2\, sinx<0\\\\\sqrt2\, sinx\cdot (\sqrt2\, sinx-1)<0\\\\t=sinx\; ,\; |t|\leq 1\; \; ,\; \; \sqrt2\, t\cdot (\sqrt2\, t-1)<0\; \; ,\; \; +++(0)---(\frac{1}{\sqrt2} )+++\\\\0<t<\frac{1}{\sqrt2} \; \; \; \Rightarrow \; \; 0<sinx<\frac{\sqrt2}{2}\; \; \Rightarrow \; \; \left \{ {{sinx>0} \atop {sinx<\frac{\sqrt2}{2}}} \right." align="absmiddle" class="latex-formula">
2\\\\2(1-sin^2x)+\sqrt2\, sinx-2>0\\\\2-2\, sin^2x+\sqrt2\, sinx-2>0\\\\2sin^2x-\sqrt2\, sinx<0\\\\\sqrt2\, sinx\cdot (\sqrt2\, sinx-1)<0\\\\t=sinx\; ,\; |t|\leq 1\; \; ,\; \; \sqrt2\, t\cdot (\sqrt2\, t-1)<0\; \; ,\; \; +++(0)---(\frac{1}{\sqrt2} )+++\\\\0<t<\frac{1}{\sqrt2} \; \; \; \Rightarrow \; \; 0<sinx<\frac{\sqrt2}{2}\; \; \Rightarrow \; \; \left \{ {{sinx>0} \atop {sinx<\frac{\sqrt2}{2}}} \right." alt="2\, cos^2x+\sqrt2\, sinx>2\\\\2(1-sin^2x)+\sqrt2\, sinx-2>0\\\\2-2\, sin^2x+\sqrt2\, sinx-2>0\\\\2sin^2x-\sqrt2\, sinx<0\\\\\sqrt2\, sinx\cdot (\sqrt2\, sinx-1)<0\\\\t=sinx\; ,\; |t|\leq 1\; \; ,\; \; \sqrt2\, t\cdot (\sqrt2\, t-1)<0\; \; ,\; \; +++(0)---(\frac{1}{\sqrt2} )+++\\\\0<t<\frac{1}{\sqrt2} \; \; \; \Rightarrow \; \; 0<sinx<\frac{\sqrt2}{2}\; \; \Rightarrow \; \; \left \{ {{sinx>0} \atop {sinx<\frac{\sqrt2}{2}}} \right." align="absmiddle" class="latex-formula">