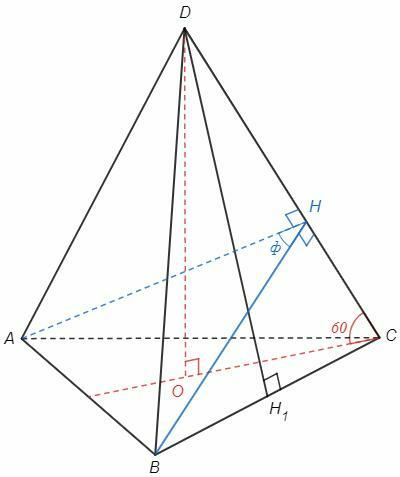
BH⊥DC, △BDC=△ADC => AH⊥DC
∠AHB=ф - искомый угол.
O - центр основания, CO - радиус описанной окружности.
BC=a, CO=a/√3
В правильной пирамиде вершина проецируется в центр основания. △DCO c углами 60, 90
DC=2CO =2/√3 a
DH1⊥BC, △DCH1, по теореме Пифагора
DH1= √(DC^2 -BC^2/4) =√(4/3 -1/4) a =√(13/12) a
△CBH~△DCH1
BH= BC/DC *DH1 =√3/2 *√(13/12) a =√13/4 a
AH=BH, △AHB, по теореме косинусов
AB^2= 2BH^2(1-cosф) <=> a^2= 2 *13/16 a^2 *(1-cosф) <=>
cosф= 1 -8/13 =5/13
∠AHB= arccos(5/13) ~67,38