Области определения и значений все числа.
Функция нечётная т.к. f(x)= -f(-x)
Найдём точки пересечения с осями координат.
(0;0)\\f(x)=0;x(x^2-3)=0;x(x-\sqrt{3})(x+\sqrt{3})=>(-\sqrt{3};0)and(0;0)and(\sqrt{3};0)" alt="f(x)=x^3-3x\\f(x)=0^3-3*0=0=>(0;0)\\f(x)=0;x(x^2-3)=0;x(x-\sqrt{3})(x+\sqrt{3})=>(-\sqrt{3};0)and(0;0)and(\sqrt{3};0)" align="absmiddle" class="latex-formula">
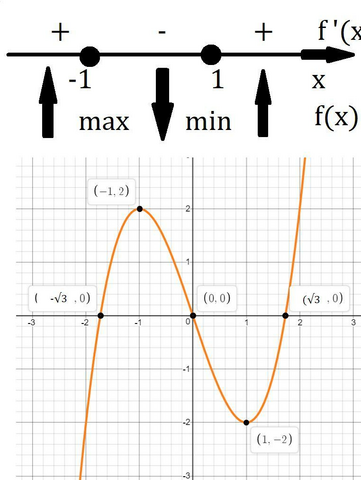
Найдём промежутки возрастания, убивания и экстремумы функции.
Смотри внизу.
Найдём координаты min и max.
(-1;2)\\f(1)=1-3=>(1;-2)" alt="f(-1)=-1+3=2=>(-1;2)\\f(1)=1-3=>(1;-2)" align="absmiddle" class="latex-formula">
Найдём точки перегиба.
Соответственно 0 это точка перегиба x<0 функция выпукла вверх</p>
x>0 функция выпукла вниз.
Координаты точки перегиба: 
(0;0)" alt="f(0)=0=>(0;0)" align="absmiddle" class="latex-formula">
Можем строить график функции.
