Ответ:
Пошаговое объяснение:
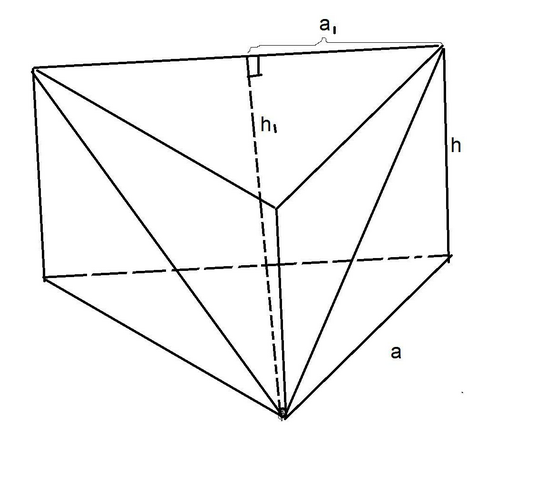
сечением является равнобедренный треугольник у которого основанием является сторона верхнего основания призмы а боковая сторона диагональ боковой грани
так как боковая грань является прямоугольником то к диагонали можно применить теорему Пифагора
d²=a²+h²=24²+12²
высота сечения h₁ образует с диагональю d прямоугольный треугольник в котором второй катет a₁=a/2=24/2=12 см
d²=h₁²+a₁²
h₁²=d²-a₁²=24²+12²-12²=24²
h₁=24 см
площадь сечения S =a₁*h₁=12*24=288 cм²