Ответ:
12869
Пошаговое объяснение:
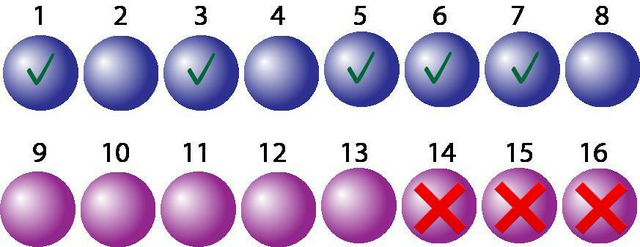
Занумеруем мальчиков числами от 1 до 8, а девочек – от 9 до 16. Выберем случайно 8 чисел из множества от 1 до 16 и будем трактовать этот выбор таким образом: выбранные числа от 1 до 8 – номера мальчиков, которых мы выбрали; выбранные числа от 9 до 16 – номера девочек, которых мы не выбрали. Автоматически получится, что выбранных девочек столько же, сколько и выбранных мальчиков.
Таким образом, число способов равно числу способов выбрать 8 элементов из 16-элементного множества, то есть  , минус 1 – вариант, когда мы не выбрали никого, нас не устраивает
, минус 1 – вариант, когда мы не выбрали никого, нас не устраивает