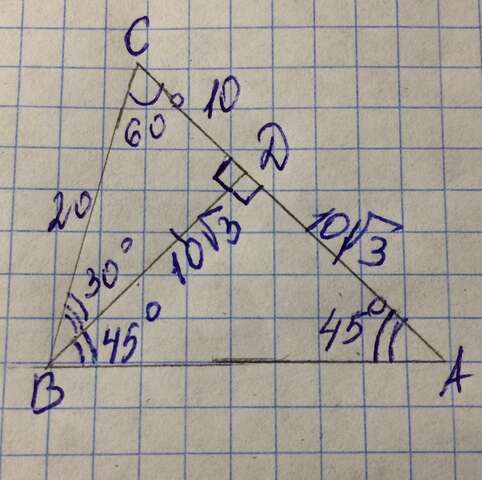Дано: ∠ACB=60°; ∠CAB=45°; BC=20.
Найти: AC=?
Решение: 1) Опустим высоту из ∠В на сторону АС в точку D. От этого ΔABC делится на два прямоугольных треугольника - ΔCDB и ΔBDA.
2) рассмотрим ΔCDB. Так как ∠CDB=90°; ∠BCD=60°, то ∠CBD=180°-(60°+90°)=30°
3) Так как BC=20, и при этом является гипотенузой, то катет напротив ∠CDB=30° будет равен половине гипотенузы:  \frac{1}{2} *20=10" alt="CD=\frac{1}{2}BC=>\frac{1}{2} *20=10" align="absmiddle" class="latex-formula">
\frac{1}{2} *20=10" alt="CD=\frac{1}{2}BC=>\frac{1}{2} *20=10" align="absmiddle" class="latex-formula">
4) Для дальнейшего решения задачи нам необходимо узнать сторону BD. Для этого можно использовать теорему синусов. В данном случае нам пригодится синус угла, противолежащего стороне BD, а именно угла BCD, который равен 60°. Табличное значение  . Для нахождения применим метод пропорций:
. Для нахождения применим метод пропорций:  x=10\sqrt{3}" alt="\frac{x}{20} =\frac{\sqrt{3} }{2} => x=10\sqrt{3}" align="absmiddle" class="latex-formula">.
x=10\sqrt{3}" alt="\frac{x}{20} =\frac{\sqrt{3} }{2} => x=10\sqrt{3}" align="absmiddle" class="latex-formula">.
5) рассмотрим ΔBDA. Так как ∠BDA=90°, ∠DAB=45°; то ∠DBA=45°.
Если ∠DAB=∠DBA=45°, то ΔBDA равнобедренный с основанием BA
6) Так как ΔBDA равнобедренный, то стороны BD и DA равны. Нам известна сторона BD, равная 10√3, следовательно BD=DA=10√3.
7) Чтобы найти сторону CA, необходимо сложить значения сторон СD и DA, равные 10 и 10√3 соответственно: 
Ответ: CA=10√3+10=10(1+√3)