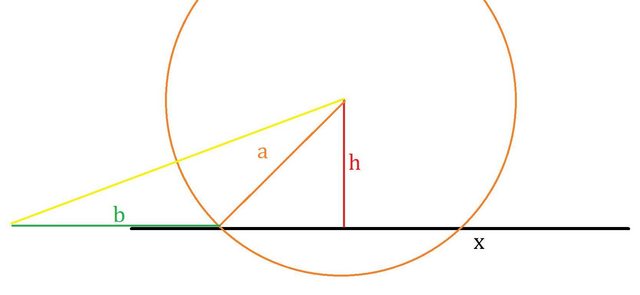
b-основание треугольника; a-сторона треугольника; h-высота опущенная на основание треугольника из его вершины.
Алгоритм следующий:
1. Чертим любую прямую х.
2. В любой точке это восстанавливаем перпендикуляр длиной h (это как бы высота к основанию).
3. Из вершины этой высоту проводим окружность радиусом a, если значения треугольника не противоречат друг другу, то окружность пересечёт прямую в 2ух точках или в 1ой.
4. Соединяем вершину высоты с любой точкой пересечения окружности с прямой х, таким образом мы получаем сторону треугольника (a).
5. В любую сторону, но на прямой х, проводим отрезок b, из точки пересечения стороны a с х.
6. Соединяем конец этого отрезка с вершиной высоты.
Имеем: т.к. сторона b лежит на прямой х, то h⊥b, ну а все остальные стороны мы указали как надо было, получился необходимый треугольник.
Примечание: когда окружность пересекает прямую х в двух точках, выбор точки не зависит от того какой треугольник получится. Если окружность пересекает в 1ой точке, то получится прямоугольный треугольник. Треугольники могут получится разными в зависимости от того в какую сторону будет проведён отрезок b. Для удобства последовательность действий в радужном порядке.