Круговой сектор ограничен радиусами, равными 5 см и дугой в 90°. Найдите площадь круга, вписанного в этот сектор. Найдите площадь круга, вписанного в этот сектор.
Вариант решения.
Ответ: S=4.289π см² * * *
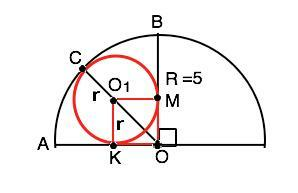
Обозначим сектор АОВ, центр вписанной окружности О1, точки касания вписанной окружности со сторонами сектора – К на ОА и М на ОВ, с дугой АВ – т.С. (см. рисунок в приложении)
Центр вписанной в угол окружности лежит на его биссектрисе,⇒ ∠АОО1=90°:2=45° .
Четырехугольник ОКО1М - квадрат, его диагональ ОО1=ОС-СО1=R-r, В ∆ ОКО1 катет КО1=ОО1•sin45°,а т.к. КО1=r, искомый r=(R-r)•√2/2 ⇒ 2r=R√2-r√2 ⇒2r+r√2=R√2. Из этого уравнения r=R√2:(2+√2). Домножив числитель и знаменатель дроби на (2-√2), по формуле сокращенного умножения получим r=R√2•(2-√2):(4-2)⇒ r=R(√2-1). Т.к. R=5 по условию, r=2,07. Формула площади круга S=πr² ⇒ S=4.289π см²