Теория вероятности. 30 % приборов собирается из деталей первого сорта, 45 % приборов...

Question

74 просмотров

Теория вероятности. 30 % приборов собирается из деталей первого сорта, 45 % приборов собирается из деталей второго сорта, остальные - из деталей третьего сорта. В первом случае надежность прибора равна 0.9, во втором его надежность 0.7, а в третьем - 0.8. Прибор в течение времени Т работал безотказно. Чему равна вероятность того, что он собран из деталей третьего сорта.

Алгебра Waterstraiker_zn (112 баллов) 02 Июнь, 20 | 74 просмотров

Дан 1 ответ

Правильный ответ

100% - 30% - 45% = 25% приборов собирается из деталей третьего сорта.

Обозначим событие А — прибор окажется надёжным.

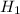$H_1$ — прибор из деталей первого сорта;

$H_2$ — прибор из деталей второго сорта;

$H_3$ — прибор из деталей третьего сорта.

Из условия проценты переводим в вероятности

$P(H_1)=0.3\\ P(H_2)=0.45\\ P(H_3)=0.25$

Условные вероятности:

$P(A|H_1)=0.9\\ P(A|H_2)=0.7\\ P(A|H_3)=0.8$

Вероятность того, что прибор собран из деталей третьего сорта, по формуле Байеса, равна:

$P(H_3|A)=\dfrac{P(A|H_3)P(H_3)}{P(A)}=\dfrac{P(A|H_3)P(H_3)}{P(A|H_1)P(H_1)+P(A|H_2)P(H_2)+P(A|H_3)P(H_3)}=\\ \\ \\ =\dfrac{0.8\cdot0.25}{0.9\cdot0.3+0.7\cdot0.45+0.8\cdot0.25}=\dfrac{40}{157}$

_zn (654k баллов) 02 Июнь, 20