Два угла треугольника равны 10∘ и 70∘ соответственно. Найдите величину угла между высотой...

Question

Два угла треугольника равны 10∘ и 70∘ соответственно. Найдите величину угла между высотой и биссектрисой, проведёнными из вершины третьего угла треугольника.

Answer 1

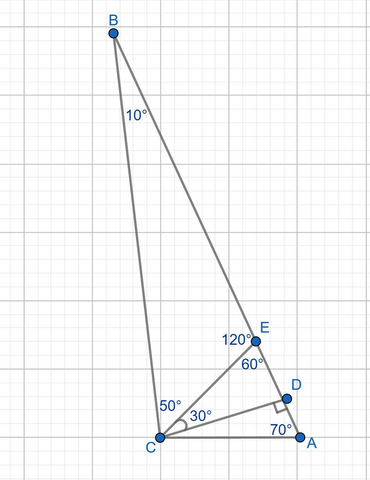
В ΔABC  ∠В = 10°, ∠A = 70°, ⇒∠BCA = 180° - 70° - 10° = 100°. Биссектриса СЕ делит ∠BCA на два угла по 50°.

В ΔBCE  ∠BEC = 180° - 10° - 50° = 120°.

Смежный с ним угол CED = 180°-120° = 60°.

В ΔECD ∠CDE = 90° (CD - высота), ∠CED =  60°. Тогда угол между высотой и биссектрисой  ∠ECD = 180° - 90° - 60° = 30°.

Ответ: 30°.

---