К окружностям с центрами О и О(1) и радиусами R и R(1) проводится общая внутренняя... - Все ответы

49 просмотров

К окружностям с центрами О и О(1) и радиусами R и R(1) проводится общая внутренняя касательная. Найдите длину этой касательной если: О О(1) = 25 см, R = 8 см, R(1) = 7 см. Помогите решить ясно с хорошим решением. Завтра кр, надо понять как это решать)))

Геометрия Daryamiass05_zn (121 баллов) 02 Июнь, 20 | 49 просмотров

Дан 1 ответ

Ответ:

20 см

Объяснение:

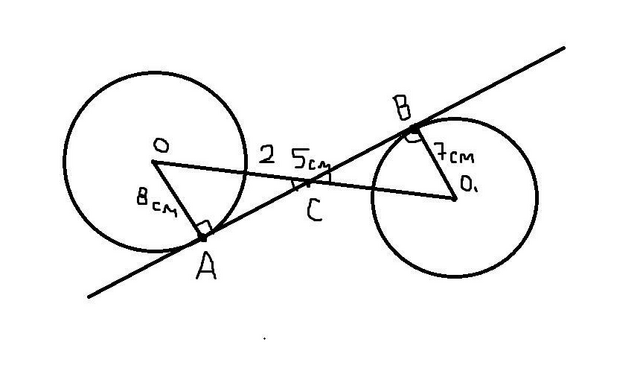
Пусть касательная - это AB, а точка пересечения пересечения касательной и ОО₁ - это точка С.

∠ОСА=∠О₁СВ как вертикальные

Так как касательная перпендикулярна к радиусу, то

∠ОАС=∠О₁ВС=90°

Отсюда треугольники АСО и ВСО₁ подобны по 2-ум углам ⇒

$\frac{OA}{O_{1}B}=\frac{OC}{O_{1}C}$

Подставим значения радиусов и выразим OС как 25 см - O₁C:

$\frac{8}{7}=\frac{25-O_{1}C}{O_{1}C}$

$\frac{8}{7}=25-O_{1}C$

$\frac{15}{7}O_{1}C=25$

$O_{1}C=25*\frac{7}{15}=\frac{35}{3}=11\frac{2}{3}$

$OC=25-O_{1}C=25-11\frac{2}{3}=13\frac{1}{3}$

Воспользуемся теоремой Пифагора и найдём АС:

АС²=ОС² - ОА²

$AC=\sqrt{(13\frac{1}{3})^{2}-64}=\sqrt{\frac{1600-576}{9}}=\sqrt{\frac{1024}{9}}=\frac{32}{3}=10\frac{2}{3}$

Используя коэффициент подобия найдём ВС:

$\frac{AC}{BC}=\frac{8}{7}$

$BC=\frac{7}{8}*AC=\frac{7}{8}*\frac{32}{3}=\frac{28}{3}=9\frac{1}{3}$

Найдём касательную АВ, зная, что АС и ВС:

$AB=AC+BC=10\frac{2}{3}+9\frac{1}{3}=20$

MynameSvetaSun_zn (2.6k баллов) 02 Июнь, 20