Помогите с алгёброй(heeeeeeeeeeelp!). номер 372

Question

Дан 1 ответ

Правильный ответ

Ответ: 1,25 .

Объяснение: $y=6x-x^2$ .

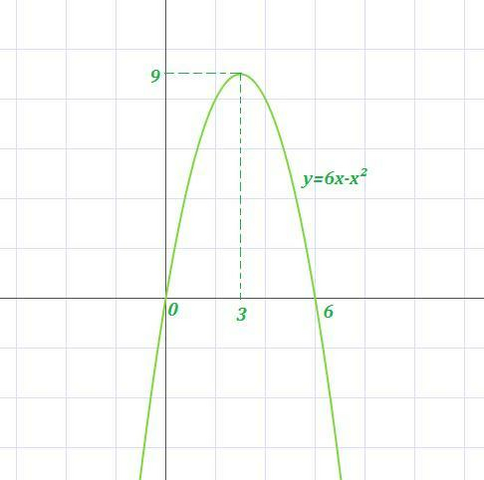
Графиком уравнения является парабола, ветви которой направлены вниз , значит максимум функции достигается в вершине параболы (см. рисунок). Координаты вершины будут (3;9), так как

х(верш.)=-b/2a=-6/-2=3 , у(верш)=6·3-3²=18-9=9 .

И тогда уравнение касательной, проходящей через точку максимума функции будет у=9. ( Минимума на всей области определения (х∈R) у такой функции не будет (см. график...), поэтому в условии описка насчёт минимума).

Составим уравнение касательной к графику функции в точке х₀= -2 .

$y'(x)=6-2x\; ,\; \; y'(-2)=6-2\cdot (-2)=6+4=10\\\\y(-2)=6\cdot (-2)-(-2)^2=-12-4=-16\\\\y=y(x_0)+y'(x_0)\cdot (x-x_0)\\\\y=-16+10\cdot (x+2)\\\\\underline {y=10x+4}\; \; \; \to \; \; (\; y(0)=4\; ;\; \; \; 10x+4=0\; \to \; x=-\frac{2}{5}\; )$

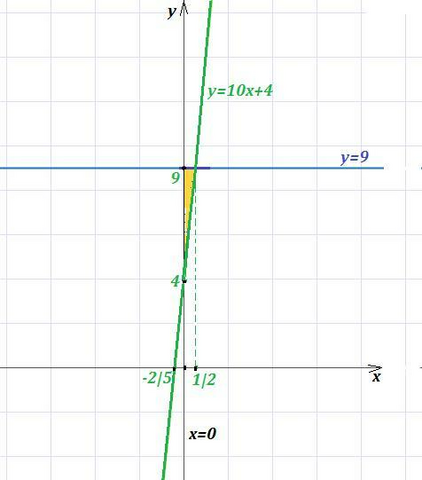
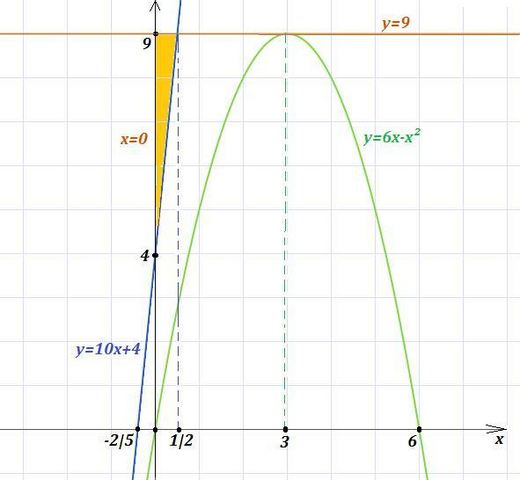
Найдём площадь треугольника, образованного осью ординат (х=0) и двумя касательными: у=10x+4 и у=9 . Найдём абсциссу точки пересечения двух касательных: 10х+4=9 ⇒ 10х=5 , х=1/2 .

На чертеже видео, что треугольник прямоугольный с катетами, равными 5 и $\frac{1}{2}$ .

$S=\frac{1}{2}\cdot 5\cdot \frac{1}{2}=\frac{5}{4}=1,25$

NNNLLL54_zn (835k баллов) 02 Июнь, 20