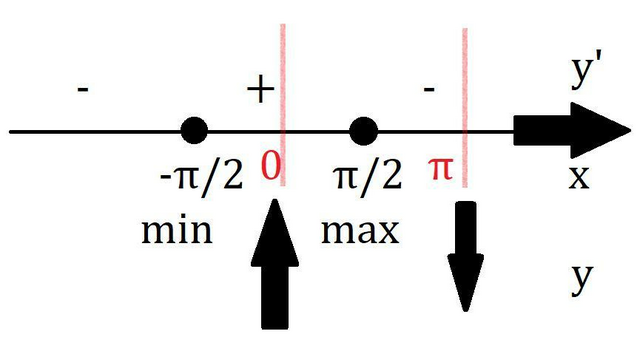
Найдём экстремумы и выделим нужный отрезок.

Значит экстремумы только в точках cos x =0
Значение в скобке всегда положительное.
См. вниз.
 \\f(x)_{min}=f(0)=f(\pi)=1" alt="f(x)_{max}=f(\pi/2)=5-1=4\\f(0)=5*0+1=1;f(\pi)=5*0+1=1=>\\f(x)_{min}=f(0)=f(\pi)=1" align="absmiddle" class="latex-formula">
\\f(x)_{min}=f(0)=f(\pi)=1" alt="f(x)_{max}=f(\pi/2)=5-1=4\\f(0)=5*0+1=1;f(\pi)=5*0+1=1=>\\f(x)_{min}=f(0)=f(\pi)=1" align="absmiddle" class="latex-formula">
Ответ: Минимальное: 1.
Максимальное: 4.