Разложим на множители выражения из числителя и знаменателя.
Таким образом
0<=>\frac{(x-1)(x-3)}{(x+3)(x-1)}>0" alt="\frac{x^2-4x+3}{x^2+2x-3}>0<=>\frac{(x-1)(x-3)}{(x+3)(x-1)}>0" align="absmiddle" class="latex-formula">
Уберём одинаковые корни
0}} \right." alt="\left \{ {{x\neq 1} \atop {\frac{x-3}{x+3} >0}} \right." align="absmiddle" class="latex-formula">
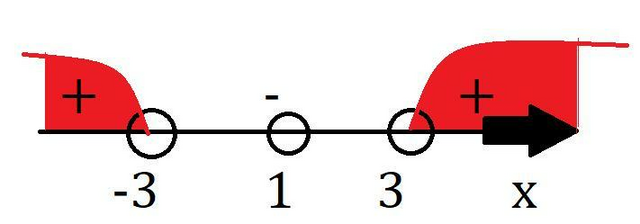
Используем метод интервалов, чтобы найти значения удовлетворяющие неравенству, см. ниже, я сразу же отметил ещё, что х≠1.
Ответ: x∈(-∞;-3)∪(3;+∞)
