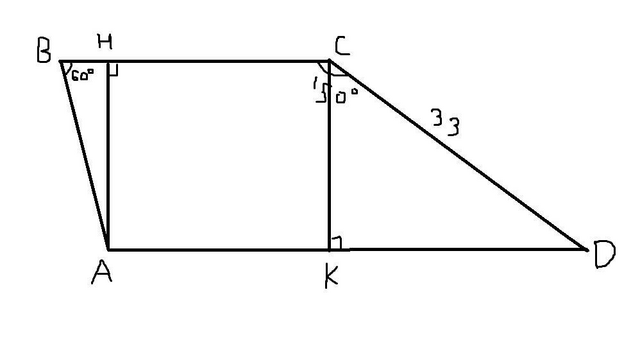
Решение:
Проведём высоты АН и СК. Высота СК разделит ∠BCD на 2 угла равным 90° и 60°. Найдём высоту СК:
cos∠KCD=CK/CD ⇒ CK=cos∠KCD × CD=1/2 × 33=33/2
Высота СК и высота АН равны ⇒ АН=33/2
Найдём боковую сторону АВ:
sin∠ABH=AH/AB ⇒ AB=AH ÷ sin∠ABH=33/2 ÷ √3/2=33/√3=33√3/3=11√3
Ответ: 11√3