Ответ:
AB=15 см, BC=10 см, CD=9 см, DA=22 см
Пошаговое объяснение:
Дано:
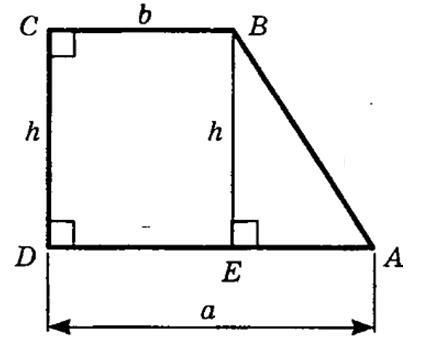
ABCD - трапеция (см. рисунок)
∠B=∠D=90°
Sтрапеция = 144 см²
h=CD=BE=9 см
a=b+12 см
Найти: AB, BC, CD, DA.
Решение.
Площадь трапеции определяется через основания и высоте по формуле:

Учитывая заданные значения, имеем

a+b=2·(144:9)
b+12+b=32
2·b=20
BC=b=10 см
Тогда DA=a=b+12 см = 10 см + 12 см= 22 см.
Известно: h=CD=BE=9 см.
Остается найти AB.
Так как треугольник ABE прямоугольный, то по теореме Пифагора
AB²=BE²+EA².
Но BE=9 см, EA=DA-BC= 22 см - 10 см = 12 см. Тогда
AB²=9²+12² = 81+144=225=15² или
AB=15 см.
Ответ: AB=15 см, BC=10 см, CD=9 см, DA=22 см.