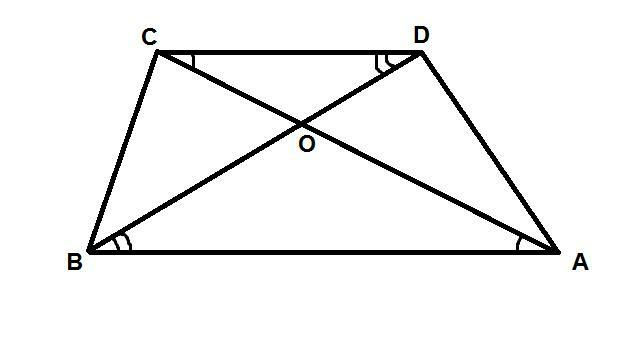
Решение:
Так как AB║DC (как основания трапеции ABCD), то ∠АВD=∠CBD и ∠BAC=∠DCA как накрест лежащие.
Отсюда ΔАВО подобен ΔDOC по 2-ум углам.
Отношение периметров подобных треугольников равно коэффициенту подобия ⇒ k=PΔABO/PΔDOC=3/2
BO/OD=3/2 ⇒ BO=3/2 OD
BD=BO + OD=30 см
5/2 OD=30 см
OD=30 см × 2/5=12 см
ВО=3/2 OD=3/2 × 12 см=18 см
Ответ: 18 см и 12 см