Ответ:
Пошаговое объяснение:
запишем уравнение в виде
2х²+ух-(у²+5)=0
и решим его относительно х
d=y²+4*2(y²+5)=y²+8y²+40=9y²+40
x₁₋₂=(-y±√d)/4
чтобы х и у были целыми числами необходимо чтобы корень из дискриминанта был целым числом и выражение -y±√d было кратно 4
решим задачу методом подбора
придавая у значения равные целым числам будем вычислять дискриминант, и если он целый то вычислим корни если они целые то все хорошо
для примера рассмотрим целые значения у ∈[-10;10]
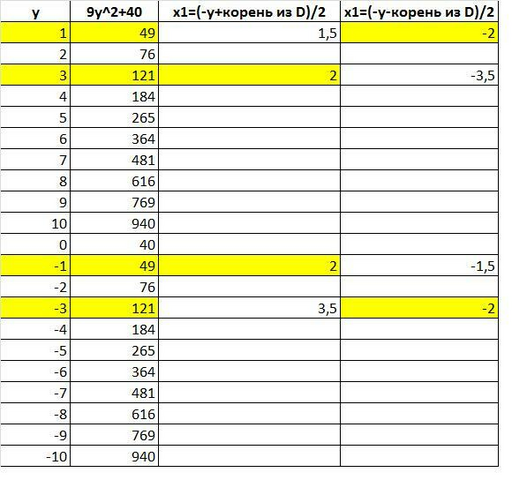
результат вычислений в приложении
полученные решения
(-2;1) (2;3) (2;-1) (-2;-3)
проверка
-2-1+8=5
6-9+8=5
-2-1+8=5
6-9+8=5
примечания
расчеты произведены в екселе,
если есть время и желание можно продолжить процесс поиска других корней но выскажу гипотезу что больше целочисленных решений нет