Ответ:
36π
Объяснение:
Шар называется вписанным в конус, если он касается всех образующих конуса и основания конуса.
Vшара=(4/3)*πr³
r - радиус шара
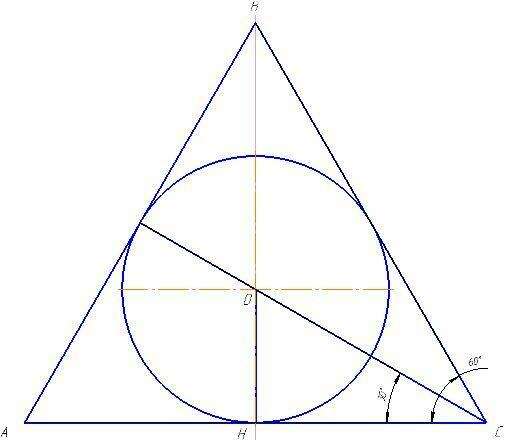
в сечении конуса через вершину и центр окружности основания в данной задаче мы имеем равносторонний треугольник, т.к. две стороны равны(они же являются образующими) и угол наклона образующий к основанию равен 60..центр окружности шара вписанного в такой конус будет лежать на пересечении двух высот треугольника ABC.
из прямоуг-го треуг-ка ВСH, зная что ВС-образующая и равна 6√3, а угол ВСH=60 градусам, т.к. образующая наклонена к плоскости основания под углом 60 градусов, найдем чему равна сторона HC,
cos60=HC/BC значит HC=cos60*BC=(1/2)*(6√3)=3√3
зная что в равностороннем треугольнике высота и биссектриса равны, то угол HCO=уголС/2=60/2=30градусов
из прямоугольного тругольника OHC найдем OH (это и есть радиус шара)
OH/HC=tg30; ОH=HC*tg30=3√3*(1/√3)=3
Найдя радиус шара можно найти ее объем:
Vшара=(4/3)*πr³=(4/3)π*3³=36π
(можно перемножить на π=3,14, тогда объем будет равен 113,04...)