Ответ:
Пошаговое объяснение:
В обеих задачах одно и то же решение.
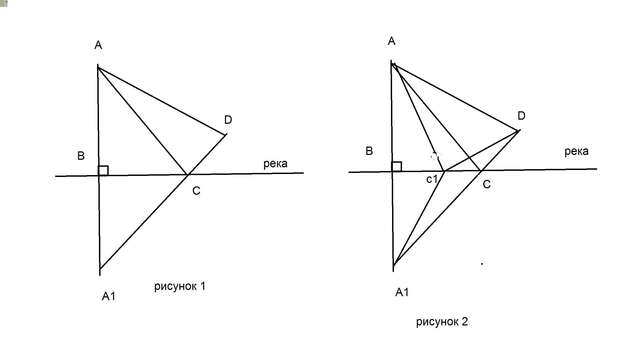
Чтобы найти кратчайшее расстояние построим следующий чертеж
от точки А проведем перпендикуляр АВ к реке и продолжим его дальше
отложим на нем по другую сторону реки отрезок А₁В=АВ
соединим точки А₁ и D отрезок А₁D пересекает реку в точке С .
так как треугольники АВС и А₁ВС равны (по двум катетам) то АС=А₁С
тогда DС+АС=А₁С+DС
поскольку кратчайшее расстояние между двумя точками есть прямая линия то минимальное значение DC+АC равно отрезку АD₁
Резюме чтобы сумма расстояний от деревень до реки была минимальной надо построить точку А₁ симметричную деревне А относительно реки по другую сторону реки и соединить ее с деревней D точка пересечения отрезка А₁D и реки и есть искомая точка С , Рис1.
на рисунке 2 видно что если взять любую другую точку то сумма расстояний до деревень будет больше