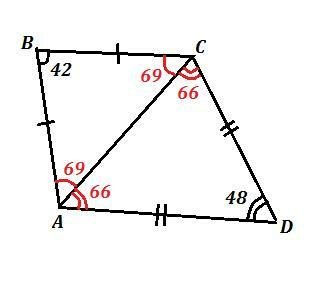
ABCD - выпуклый четырёхугольник , ∠В=42° , ∠D=48° , АВ=ВС , AD=CD .
Проведём диагональ АС. Получим два равнобедренных треугольника: ΔАВС и ΔACD . Углы при основании равнобедренного треугольника равны, а сумма углов в треугольнике равна 180°. Из этого следует, что
∠ВАС=∠ВСА=(180°-42°):2=69° , ∠CAD=∠ACD=(180°-48°):2=66°
∠А=∠ВАС+∠CAD=69°°+66°=135