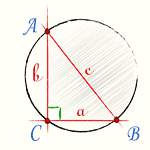
Есть такая теорема:
Диаметр описанной окружности прямоугольного треугольника лежит на гипотенузе этого треугольника.
Значит, радиус описанной окружности равен 1/2 гипотенузы треугольника ABC, т.е. r=AB/2.
Рассмотрим треугольник ABC:
1). Пусть угол A=x градусов, тогда, по условию задачи, угол B=2x градусов, значит,
x+2x=90 (т.к. сумма острых углов прямоугольного треугольника равна 90 градусам),
3x=90,
x=30 градусам.
2). Против бОльшего угла лежит бОльшая сторона, значит, AC-больший катет, а по условию, он равен 4√3.
Из (1) и из теоремы (В прямоугольном треугольнике против угла в 30 градусов, лежит катет, равный половине гипотенузы), значит:
если обозначим BC=x, тогда AB=2x, можем составить уравнение:
(4√3)²+x²=(2x)² (по теореме Пифагора),
16·3+x²=4x²
48=4x²-x²
48=3x²
x²=16
x=4
BC=4, AB=2·4=8
r=AB/2=4