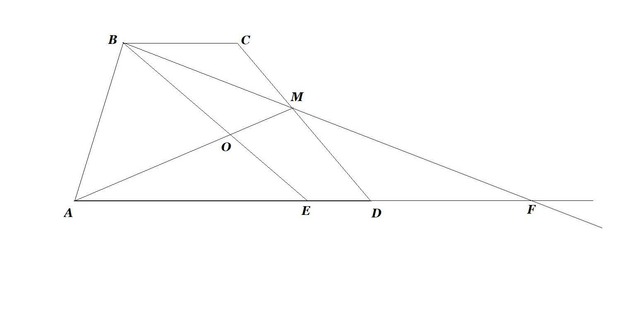
Начертим отрезок BM и продлим его за точку M до пересечения с прямой AD; Точку пересечения обозначим за F;
Вполне очевидно, что треугольники MDF и BCM равны, откуда следует равенство BM = MF; Значит AM - медиана в треугольнике BFA; Поскольку точка O делит эту медиану в отношении 2:1 начиная с вершины, то BE - также медиана этого треугольника. Следовательно, AE = EF = AF/2 = (AD+DF)/2 = (AD+BC)/2 = (126+92)/2 =109; Надеюсь, из рисунка все станет ясно.