Вариант решения.
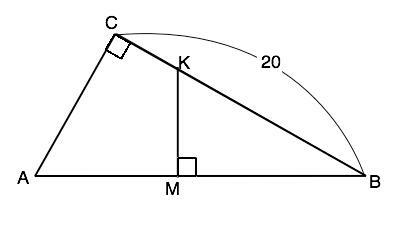
Пусть в треугольнике АВС ∠С=90°, В - вершина меньшего острого угла, а КМ – перпендикуляр к гипотенузе. Расстояние от точки до прямой равно длине перпендикуляра между ними. Искомый отрезок - ВМ.
Δ АВС подобен Δ КВМ по общему острому углу СВА.
Отношение площадей подобных фигур равно квадрату коэффициента их подобия.
По условию Ѕ(АСВ):Ѕ(КВМ)=2, и это отношение равно k² . ⇒ k=√2, следовательно, ВС:BM=√2 ⇒ MB=BC:√2=20:√2=10√2 см