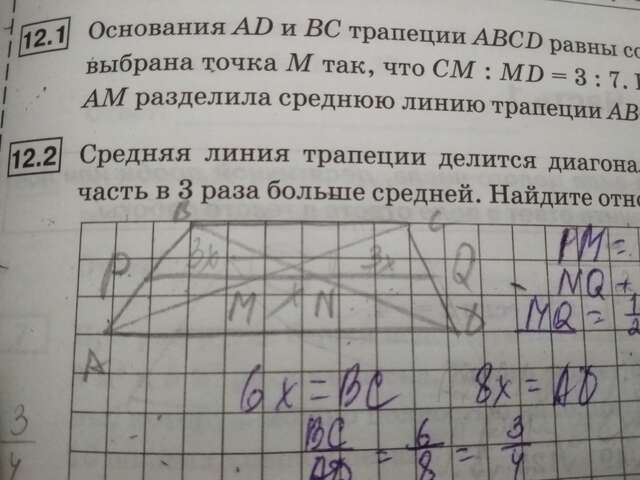
Рассмотрим ∆ ABC и АСД. В них:
PM и MQ средняя линия соответственно.
Средняя линия в треугольнике равна половине стороны, против которой лежит, следовательно:
PM = 1/2 BC -> 2PM = BC
MQ = 1/2 AD -> 2MQ = AD
По условию крайние отрезки средней линии относятся со средней частью как 3:1, поэтому мы можем взять отрезки за х:
MN - x, PM = NQ = 3x.
MQ = MN + NQ = 3x + x = 4x
Из этого исходит, что:
2PM = BC => 3x = BC
2MQ = AD => 4x = AD
У нас известны соотношения сторон, поэтому:
BC:AD = 3x : 4x
BC:AD = 3:4
Ответ: 3:4
Я сама искала ответ на эту задачу в интернете, но так и не нашла. Надеюсь, что помогла. Желаю удачи в сдаче ВПР. vendermask.