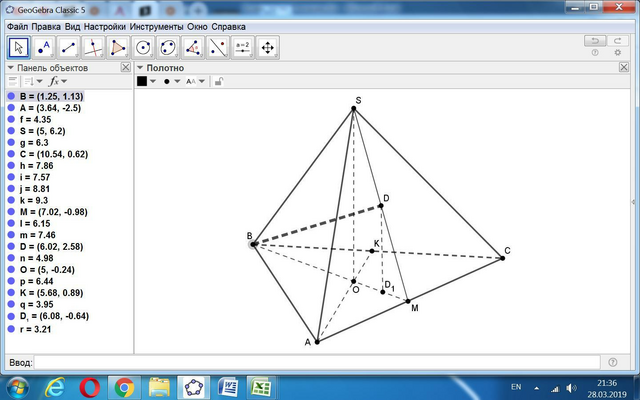
Эту задачу можно решить двумя способами: векторным и геометрическим.
1) Примем длину ребра основания пирамиды равной 2.
Поместим пирамиду вершиной В в начало, стороной ВА по оси Оу.
Определяем координаты точек B и D для вектора BD и точек S, C и К для плоскости, проходящей через ребро SC и середину ребра AB. Здесь точка К - середина ребра АВ.
В(0; 0; 0). Координаты точки D. Основание апофемы через точку D - пусть это точка М. ВМ - это высота основания h = a√3/2 = 2√3/2 = √3.
Точка D проецируется на основание (D1) как середина ОМ = (1/3)h.
Отрезок ВD1 = (2/3)h+ ((1/3)h/2) = 5h/6 = 5√3/6.
Раскладываем BD1 по осям:
Оx = (5√3/6)*cos 60° = (5√3/6)*(1/2) = 5√3/12,
Оy = (5√3/6)*cos 30° = (5√3/6)*(√3/2) = 5/4 = 1,25.
Высота пирамиды Н(S) = 2*(5/√6) = 10/√6.
Высота точки D равна половине, то есть 5/√6.
Точка D(5√3/12; 1,25; 5/√6). Это же значение вектора BD.
Точка С(√3; 1; 0). Точка S(√3/3; 1; 10/√6). Точка К(0; 1; 0).
Плоскость SCK параллельна плоскости xOz, её уравнение по трём точкам: 0x - 7,071067812y + 0z + 7,071067812 = 0.
Направляющий вектор прямой имеет вид: s = {l; m; n}
Вектор нормали плоскости Ax + By + Cz + D = 0 имеет вид n (A; B; C).
Скалярное произведение n x s = -8,838834765.
Модуль вектора BD = s = √(0,721687836² + 1,25² + 2,041241452²) = 2,5.
Модуль вектора n = 7,071067812.
Синус искомого угла равен:
sin φ = abs(n x s)/(|s|*|n|) = 0,5.
Угол равен 30 градусов.