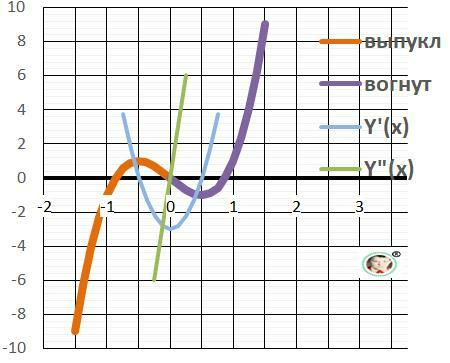
Дано: y(x) = 4*x³ - 3*x
Найти: Значения экстремумов.
Объяснение: Экстремумы в корнях первой производной.
Решение.
f'(x) = 4*3*x⁽³⁻¹⁾ - 3*x⁽¹⁻¹⁾ = 12*x² - 3 = 12*(x² - (1/4)) = 12*(x - 1/2)*(x + 1/2) = 0
Разложили на множители ми корни уравнения.
Точки экстремумов: x₁ = - 1/2, x₂ = 1/2.
Вычисляем значения экстремумов.
Ymin(0.5) = -1 - минимум - ответ.
Ymax(-0.5) = 1 - максимум - ответ.
Дополнительно.
Рисунок с графиками функции и её производных - в подарок - в приложении.