Дано: y(x) = - x² - 3x + 9 + 1/3*х⁻¹
Исследование.
1. Область определения: Член 1/(3х) - деление на 0
х ≠ 0 D(y)= X∈(-∞;0)∪(0ж+∞).
2. Вертикальная асимптота.

Разрыв II-го рода. X=0 - вертикальная асимптота.
3. Наклонная асимптота (горизонтальная):
k = lim(+∞)Y(x)/x = ∞ - асимптот - нет.
4. Пересечение с осями координат.
Пересечение с осью ОХ - нули функции,
Погрешность расчёта будет незначительной если пренебречь четвёртым членом разложения функции. Тогда получим квадратное уравнение:
- x² - 3x +9 = 0, D = 45, √45 = 3√5 и два корня: х ≈ - 4,9, х ≈ 1,9
При полном решении получаем три нуля функции
x₁ = -4,8438, x₂ = -0.036596 и x₃ = 1,8804 - (без расчёта).
Пересечения с осью ОУ - нет.
5. Интервалы знакопостоянства.
Отрицательна: Y(x)<0 - X∈(-∞;х₁]∪[x₂;0)∪[x₃;+∞).</p>
Положительна: Y>0 - X∈(x₁;x₂]∪(0;x₃] .
6. Проверка на чётность. Функция общего вида.
7. Поиск экстремумов по первой производной.
y'(x) = - 1/(3*x²) - 2*x - 3 = = -6*x³ -9*x² - 1 = 0.
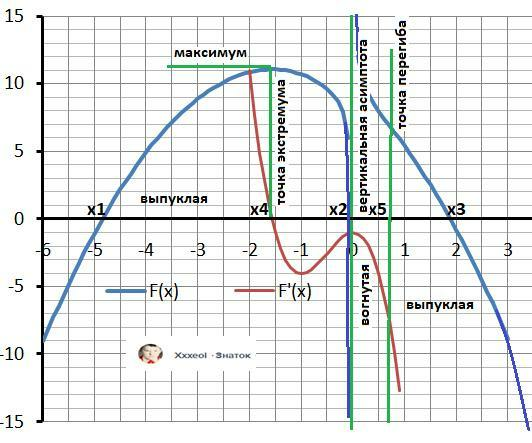
Точка экстремума : x₄ ≈ - 1,5678
8. Локальные экстремумы.
Максимум: y(x₄) ≈ 11,033.
9. Интервалы монотонности.
Возрастает - X∈(-∞;x₄].
Убывает: X∈[x₄;0)∪(0;+∞).
10. Поиск перегибов по второй производной.
y"(x) = (-6*x³+2)/(3*x³) =0
Корень уравнения: x₅ = (3²/³)/3 ≈ 2.08/3 =0.7
11. Поведение.
Выпуклая - "горка" - Х∈(-∞;0)
∪[x₅;+∞)
Вогнутая - "ложка"- X∈(0;x₅].
12. Область значений - E(y): y∈(-∞;+∞).
13. График функции на рисунке в приложении.
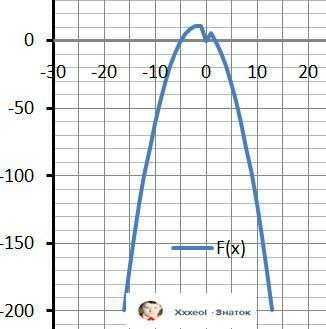
Дополнительно описание:
Смещенная отрицательная парабола с разрывов II-го рода при Х = 0. График в более крупном масштабе на рисунке в приложении.