Ответ:
Пошаговое объяснение:
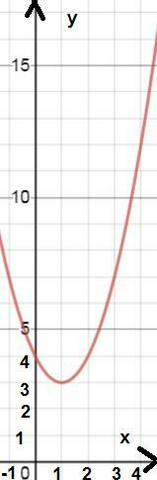
График функции y=x²-2x+4; x∈[-1;4]
1)Область определения
D(y)=R
2)Область значения
найдем координату вершины параболы
х=-b/2a=-(-2)/2=1
y(1)=1-2+4=3 ; вершина в точке (1;3)
E(y)=[3;+∞)
3)На каких промежутках возрастает и убывает
y'=2x-2=2(x-1)
при х<1 y'<0 y убывает</p>
при х>1 y'>0 y возрастает
4)Четная или нечетная
-y(x)=-x²+2x-4
y(-x)=(-x)²-2(-x)+4=x²+2x+4
y(-x)≠y(x) не является четной
y(-x)≠-y(x) не является нечетной
у(х) функция общего вида
точка пересечения с осью ОУ
х=0 ; у=4 (0;4) точка симметричная точке (0;4) относительно оси симметрии х=1 (2;4)
точки пересечения с осью ОХ
дискриминант d=4-16=-12 точек пересечения с осью ОХ нет